For many years, I have used Python and Numpy and other packages in the same ecosystem for pretty much all of my projects. However, I stumbled upon Julia and quickly discovered how nicely designed and fast it is. Coming from Python, I find Julia to be quite easy to understand. Still, there were some quirks that I had to get used to, particularly dealing with types explicitly (you don’t really need to do much of this, but this practice can speed up the code) and the way Julia handles inheritance and whatnot.

After reading the documentation and a few tutorials over a weekend, I figured the best and quickest way to get myself oriented with the language is to do something with it—and preferably that something will be similar to what I would use it for in my own work. So, this post is a by-product of that.

This article goes over writing some simulation code for an opinion dynamics model from scratch in Julia. Rather than a full-on tutorial of how Julia works, what you will mostly find in this post is a documentation—frankly, commentation—mostly for myself of why and how I wrote the code I did, from the perspective of someone coming from Python.

It turns out that the code resulting from this case study can also serve as an excellent tool for someone wanting to explore an opinion dynamics model (to be described below) without actually fidgeting with much code. I have uploaded the source code file to GitLab here and provided a short example of how you can use it. You can feel free to play around with it and try out different parameter values to see different results which are always interesting. If you have suggestions, see typos or things that aren’t correct as you read, please don’t hesitate to reach out to me.

Recommended background

While I wrote this mostly for myself, I do believe that this use case could benefit people like me who are thinking of migrating to Julia or wanting to see more examples of some simulation code. To be able to make the most out of this case study, basic (in bold because nothing fancy is needed) familiarity with Julia syntax, agent-based models, and graph theory is encouraged.

The model we’re coding

What we are simulating here is a variant of a bounded-confidence opinion dynamics model called Deffuant—Weisbuch (DW). In this model, two agents influence each other’s opinion if the difference in their opinions is less than the confidence bound c. The idea is that people have “selective biases” and tend to consider only those perspectives which do not deviate too much from their own. Indeed, the extent of how much deviation is allowed is a parameter we can control in this model, i.e. the confidence bound. In the original, basic model, individuals or agents in the system hold some opinion values, say x_i \in [0,1]. At each time step, a pair of random agents i and j meet and see if the difference in their opinions is less than the confidence bound or not. If it is, they compromise and shift their opinions closer to each other, as governed by the equations below, where \alpha \in (0,0.5] is often called the convergence parameter as it controls the speed of convergence.

x_i(t+1) = x_i(t) + \alpha(x_j(t) - x_i(t))\\
x_j(t+1) = x_j(t) + \alpha(x_i(t) - x_j(t))

If the pair of opinions turns out to be farther apart than c, nothing happens in that time period.

Since I often work with networks, I will add an element to this model such that instead of having a well-mixed population (i.e., any two agents can meet each other), we are going to have an underlying social network structure such that an agent only interacts with its social connections. The purpose of adding such an element is not only that it is a realistic assumption that agents are only mostly influenced by their connections, but also because I often need to code things like this in my own work, and so this will help me learn how to do that in Julia. The type of underlying social network will be a synthetic one, generated using the Erdos-Renyi random graph model, G(N,p), where p is the probability of an edge between some two nodes being included in the network (so when p=1 we have a complete graph).

With this network structure, we then proceed as follows: at each time step, we select q nodes uniformly at random. Each of those selected nodes then proceeds to select one of its friends, also uniformly at random, and they interact in the manner governed by the DW mechanism (that is, compromise if difference in opinions is smaller than c ).

A quick note on implementation

This may not be the most efficient or fastest simulation code you will come across for this model. The goal for me is to get the simulation working correctly, and as efficiently as someone new to Julia can possibly make it.

I have also taken some design inspirations and implementation details from Agents.jl and LightGraphs.jl. In fact, I would say that I am not really doing anything novel in this post—I merely tried to study and understand how better programmers than me have implemented these things. I could have used these packages directly to accomplish certain tasks, but the point of this is to learn the implementation itself, and not the accomplishment of the tasks.

Data structures and simulation design

To run simulations for this model, the main “classes” that we will build are

1. the Agent class; and
2. the Model class.

An instance of Agent represents, obviously, an agent/node in the system. Naturally, each agent will possess attributes such as current_opinion and neighbors (representing the list of social connections it has).

An instance of Model represents one instantiation of the model. Model contains attributes like the collection of agents in the system, as well as model parameters such as c,alpha, and q.

As opposed to Python or Java, classes in Julia do not have internal methods because Julia adopts multiple dispatch as its design philosophy. (More on this later.) So we will have separate methods that will perform actions on objects of types Agent and Model. Mainly, we will need functions to:

1. initialize_model(args)
2. run(model, args)

Of course, there will be a number of other smaller, helper functions to help us achieve these big tasks of initializing the model (which entails the creation of agents, endowing them with initial opinion values, the generation of the synthetic network), and running it (entailing selecting agents at random, updating agents’ opinions, checking for convergence, etc). Note that above, we call the second method on a Model object by passing the object as an argument, rather than doing model.run().

On with the code…

As mentioned earlier, we will first need to create a class for agents in the system. In Julia, classes or types are called struct and can contain data of any defined types you desire. It is immutable by default, but since we will be updating the agents’ opinions, it makes sense to make it a mutable struct.

The official documentation of Julia gives an explanation of why multiple dispatch is employed: say if we consider some method such as addition, it is unclear whether add() should belong to one special argument or the other. For example, should it be x.add(y), where the type of x “owns” the method add(), or should it be y.add(x)? Instead, we ought to be able to do add(x,y) just like we would naturally do in mathematics. It is then up to the programmer to do the “patchwork” (if necessary) and figure out what add(x,y) should be, depending on the “types” of x and y.

For our Agent type, we will make it contain certain fields of certain types as follows:

The code should be quite self-explanatory: we identify a given agent by its id, which is an integer field, and we have fields to keep track of an agent’s opinions at different points, as well as an array of ids of agents it’s connected to in the network.

We will also create a Model type and a constructor for it as follows:

Even though the type itself is immutable, Model.agents will be mutable since it is a field pointing to a dictionary (whose values are Agent objects and keys their ids) which is mutable.

Julia actually automatically creates a constructor function for Model for us with the number and types of arguments matching the fields inside the struct. But because the first field is of type dict, the user will actually have to pass in a dictionary of agents when instantiating a Model object if we do not define a more specific constructor. But we ought to abstract that detail away from the user for usability and other reasons. Instead, we only want them to pass the parameter values associated with the model. To create a Model object, the user will need to just call model = Model(c,alpha,q) with c, alpha, and q having the appropriate types and numerical values.

As a last note before we move on to defining methods, we did not actually have to specify the types of the fields in the classes we just created at all. Without this specification, Julia will assume that the field can contain anything (objects of type Any). But since we already know what types we will be working with, it is a good practice to be as specific as you can, but not more, so as to make the code more efficient. See Julia’s official documentation on types for this.

Naturally, we will want to be able to do things like model[id] to access the agent in the system with that id. Since Model is a custom type we created, this functionality is not native to this type. However, we can leverage Julia’s interfaces and simply extend 1 or 2 methods to do just this:

Additionally, the code above contains a method to get an iterator over all agents (agent objects) in the model by calling allagents(model).

Before we write a function to initialize the model, let’s first write a few helper functions to add agents to the model and generate the underlying social network:

In initialize_network(), we did a manual implementation of a G(N,p) random network generator, as well as a hand-implementation of how the edges are stored (the design of this is borrowed from LightGraphs.jl‘s implementation). We rely on the Distributions package to generate a Binomial random variable—which would determine how many edges we will have in our network—given M_{max}, the total number of possible edges that could exist in a graph with N nodes, and p, the probability of seeing any given edge. We then randomly generate edges (i,j) using Tuple(rand(1:N,2)). Note in Line 13 that we perform a short-circuit evaluation to ensure that we don’t have a self-loop: (i \neq j or else continue to the start of the loop again). After we make this verification, we check whether j is already in the list of i‘s neighbors by using searchsortedfirst(list,e) which returns the index after the first element in list that is greater than or equal to e, or length(list)+1 if none is found, assuming that the list is sorted (which it is, by the design of how we will insert into the list using this index). We then use insert!() to add connections to the two nodes appropriately. The ! punctuation in insert!() signifies that this function directly modifies the list.

Note the use of @inbounds, as this tells Julia to skip its internal checking of whether the indices we are using are out of bound or not. Since we enforce this by how we generate the edges, we can safely skip this step, which would greatly reduce the amount of memory and computational time needed.

Now we have all we need to write a method to initialize a Model object. At the beginning, we will endow all the agents with initial opinions that are drawn from the uniform distribution on [0,1].

At this point we are left with the details of the simulation itself (i.e., the updating of the opinions). What we will do is let the simulation run until the opinions have converged—by this I computationally mean they stay stationary for 100 consecutive steps—or until we reach a specified maximum number of steps, whichever condition is satisfied first.

The method to update agents’ opinions based on our model is quite simple—we are merely following the mechanism we have outlined above:

Note again the ! as this method directly modifies the Agent objects in the model. I find this convention in Julia to help with clarity a lot, as I no longer need to constantly look up documentation pages to see whether the operation is in-place or returns a copy of the thing I’m operating on.

To check whether an agent has shifted their opinion in each time period, we simply check if its previous opinion is different from its new opinion. This function below is what Agents.jl uses in their Hegselmann—Kraus opinion dynamics model, which essentially checks if there exists an agent whose previous and new opinions differ by more than a tolerance of 1e-12 (and if so, return false). What we need in order to reach convergence is for this method to return true for 100 consecutive steps. Why we use previous opinions instead of current opinions will be clearer in the code snippet after this next one.

Finally, we write a method to run the model and collect the data:

Above we initialize a (max_steps,N)-multidimensional array with missing values. But we also specify that this array will contain both missing (similar to NaNs in Python) and Float64 values by using the Union type Union{Missing, Float64}. Without this, Julia would infer that our array is an array with elements of type missing only, which is not what we want because we will fill the cells with agents’ opinions later as the model runs.

In contrast to what I am used to in Python and pandas, each column in a dataframe or an md-array in Julia is a series. This is why we want N columns, so that each column represents the evolution of an agent’s opinion over time. That is, each row in this array corresponds to the data from one time step.

Here I also used the “ternary operator” ? : to determine how many time steps in a row the opinion profile has stayed the same.

Results & improvements

With all this code together, we can actually finally run our model and plot some results!

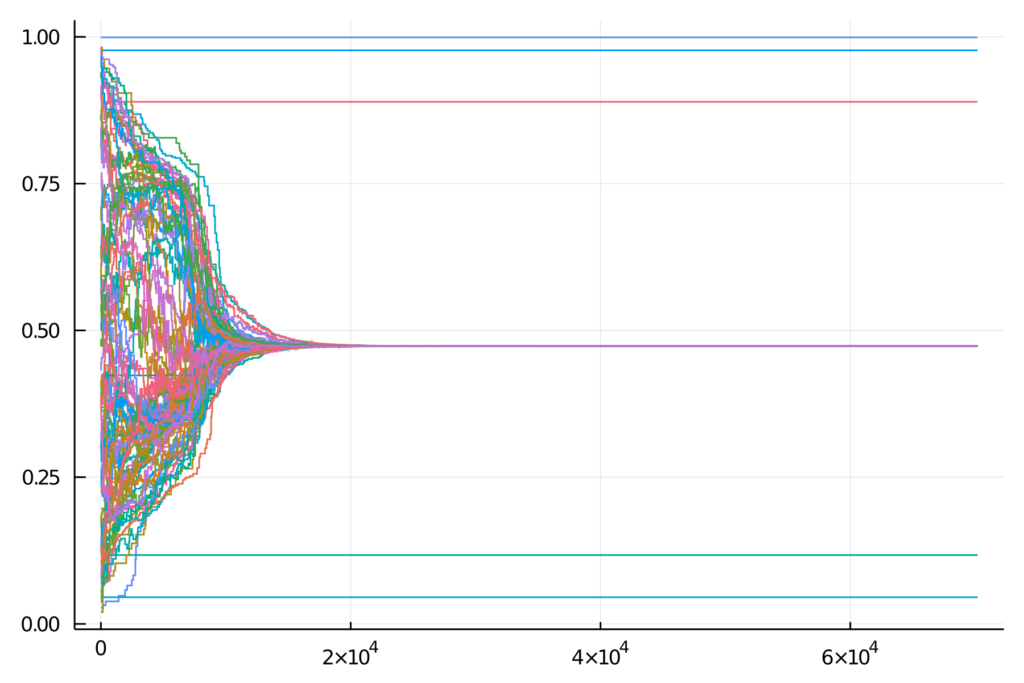
The plot we see visualizes the opinions of all agents over time. You can see that initially every one has different and random opinions. But at the end, all individual opinions converged to one single value, reaching a consensus. Since I have been working with a network-based DW model for the past number of months, I know that what we are seeing is in line with what we would expect. With sufficiently large confidence bound values, agents are open-minded enough that all of them reach consensus quickly.

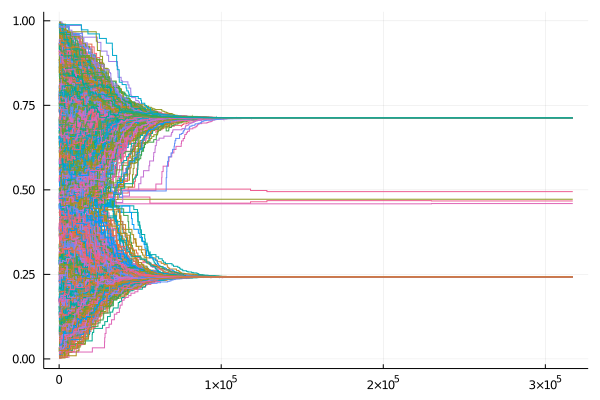
As another fun exercise, let us increase the size the system to N=1000 agents, let p=1.0 to generate a complete graph (i.e., we are recovering the original DW model) and let c=0.2 and run another simulation. (I am also going to increase the max number of steps to let it run for longer, since we have a bigger system now.) Below is a plot of what the system can wind up like. Here we are recovering the original DW model (with the assumption that agents are well-mixed instead of placed on a network), and we see that at the end agents end up aligning themselves into 2 separate opinion clusters!

Overall, I am very happy with the results. The speed that I was able to achieve with Julia really exceeds my expectations and is noticeably faster than what I can get in Python. With this basic simulation code working, some things I can do in the future to improve upon it is learn how to time and memory profile my code, as well as parallel processing in Julia so that I can run multiple trials simultaneously and collect all the data at once. Perhaps we can also try putting agents on different cores when q>1 as well to parallelize and speed things up more.

Summary

In this post, I wrote a piece of simulation code for a network-based DW model in Julia as a case study as I attempt to switch to Julia from Python. Doing the case study and writing this post has helped me understand the language design more, and I hope that it can also serve to be useful to someone else, if not just for the code itself.

Source code

I have published the source code in its entirety at this GitLab repo here: https://gitlab.com/unchitta/deffuant-weisbuch-jl/.

If you do use this code in some way, please consider referencing it.

References

• Deffuant, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87-98.
• JuliaLang’s official documentation
• Agents.jl
• LightGraphs.jl
  • LightGraphs.jl / src / SimpleGraphsCore / simplegraph.jl
    • (For studying how LightGraphs.jl implements internal storage of network structures)
  • LightGraphs.jl / src / SimpleGraphs / generators / randgraphs.jl
    • (For studying how LightGraphs.jl implements an ER graph generator)
• Learn Julia the Hard Way